Il Quadro di Riferimento (QdR) delle Prove INVALSI di Matematica è il documento ufficiale dell’INVALSI, costruito in linea con le Indicazioni nazionali e le Linee guida del MIUR, su cui si sviluppano le Prove. Oltre a definire le linee teoriche che guidano la Prove, mette a disposizione diversi esempi che possono aiutare a comprendere le competenze e le abilità legate alla literacy matematica.

Consigliamo di leggere prima Cos’è la literacy matematica
Ogni quesito delle Prove INVALSI di matematica è costruito con un preciso scopo della domanda, è esplicitamente associato a un traguardo di competenze ed è classificato in un ambito prevalente (Relazioni e funzioni, Dati e previsioni, Numeri, Spazio e figure).
Il gruppo di lavoro INVALSI, basandosi sempre sulle Indicazioni nazionali e sulle Linee guida, ha costruito un raggruppamento dei quesiti secondo tre dimensioni: Conoscere, Risolvere i problemi, Argomentare.
Con l’aiuto di 3 esempi, uno per ogni dimensione, vediamo in concreto dove e come le competenze e le abilità legate alla literacy matematica vengono costantemente richieste nella vita di tutti i giorni. Tutti e tre i quesiti sono stati somministrati ad alunni del grado 5 (ultimo anno della primaria).
Vediamo un primo esempio
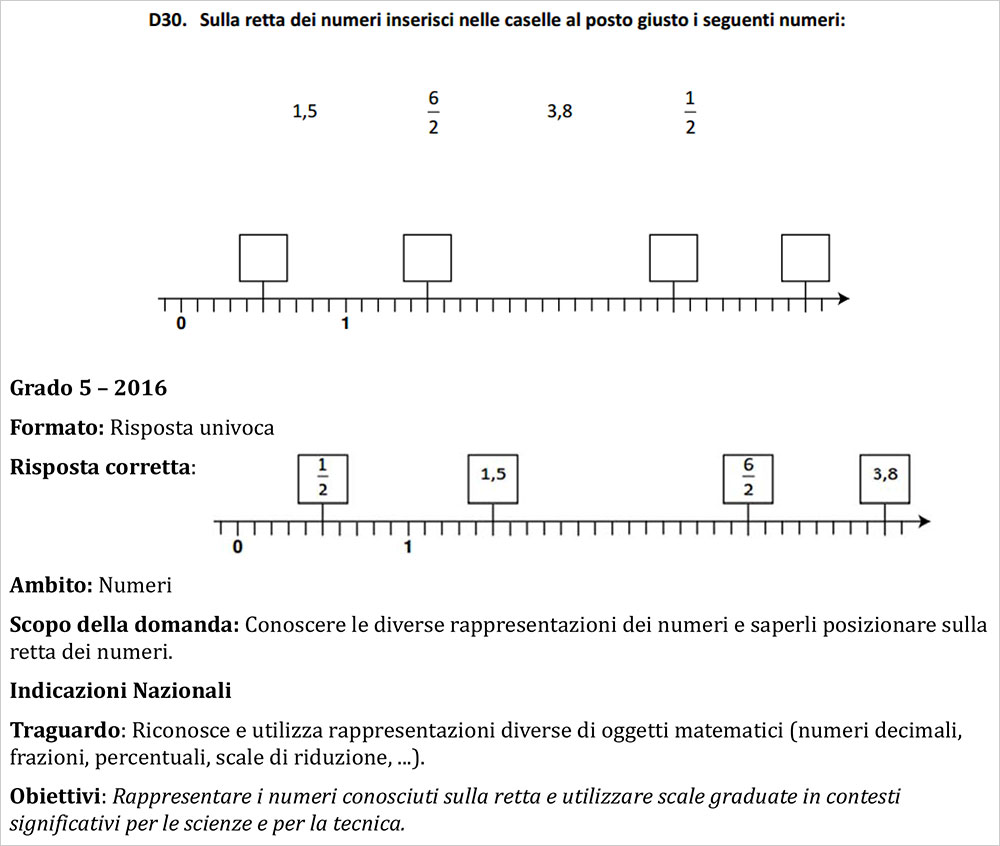
Questo quesito serve per verificare se l’alunno ha acquisito dimestichezza con le rappresentazioni dei numeri (interi, decimali, frazioni, ecc..) e se è quindi in grado di utilizzare questa competenza in contesti quotidiani, come prevede il traguardo descritto nella figura 1.
Spesso infatti gli alunni imparano le regole ma non ne colgono l’attinenza con la realtà.
Facciamo un esempio molto semplice sui numeri frazionari.
Un ragazzo potrebbe conoscere, ad esempio, le regole che gli permettono di sommare ¼ a ¼ (che fa ½), ma non cogliere la semantica dietro la sintassi, il significato dietro il simbolo numerico.
In un contesto reale, come leggere l’orologio, il senso intrinseco dei numeri frazionari è palese: un quarto d’ora più un quarto d’ora fa mezz’ora (¼ + ¼ = ½). La soluzione viene alla mente subito, senza dover richiamare regole o dover fare passaggi e semplificazioni.
Ovviamente con numeri frazionari diversi da un quarto o metà difficilmente il significato del segno numerico e la sua collocazione nella linea progressiva dei numeri (1, 2, 3, ecc…) saranno altrettanto lampanti, e conoscere le regole si rivela di nuovo indispensabile.
Ma più ancora della regola, è importante che un ragazzo alla fine della scuola primaria capisca la sequenza logica dei numeri, che sappia che 0,5 equivale a ½ (un mezzo, metà) e che quindi la sua posizione è a metà strada tra lo 0 e l’1.
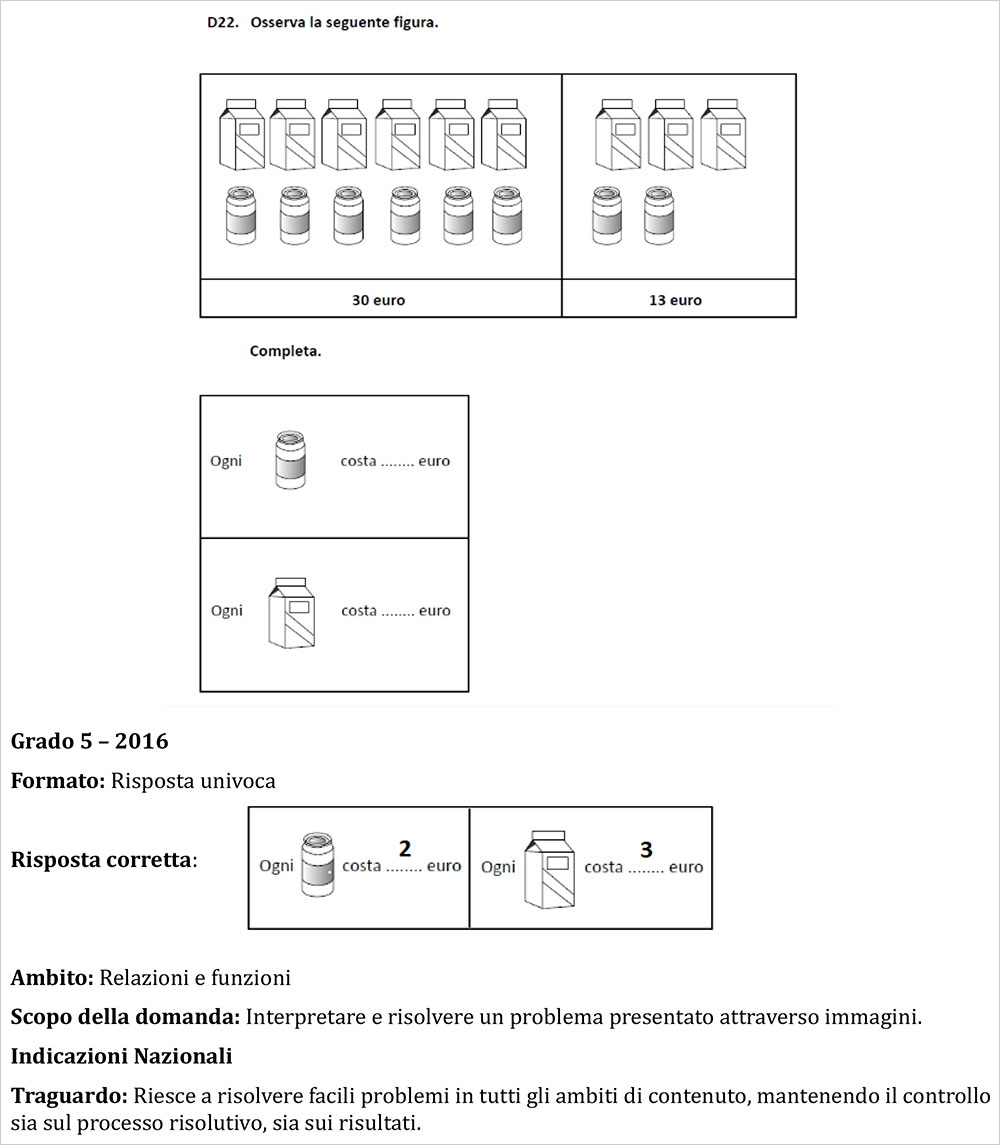
Anche questo quesito fa vedere come sia poco utile imparare le regole logico-matematiche a pappagallo, senza capirne il senso sotteso. E se le quantità invece che attraverso i numeri vengono rappresentate per immagini? L’alunno è in grado di usare gli strumenti matematici che ha acquisito per poter – per così dire – improvvisare in un contesto diverso dal solito?
L’ambito di questo quesito è infatti Relazioni e funzioni. Significa che indaga sulla capacità del ragazzo di muoversi agevolmente in contesti che hanno attinenza solo indiretta con le regole imparate.
Svolgendo l’esercizio vi accorgerete che possedere buone competenze matematiche da anche la possibilità di verificare a posteriori se la soluzione è corretta.
La mia risposta è giusta? Proviamo ad attribuire il prezzo ipotizzato al cartone (3) e alla lattina (2) e controlliamo se entrambe le somme in alto tornano:
(6×3) + (6×2) = 30? e (3×3) + (2×2) = 13?
Il bravo alunno del grado 5 non ha difficoltà a leggere, a scrivere o a capire queste operazioni. Ma quello competente non ha difficoltà nemmeno a richiamare quei calcoli partendo da immagini di lattine e cartoni del latte.
Un ultimo esempio

Come il precedente quesito, anche questo indaga l’ambito Relazioni e funzioni.
L’abilità richiesta dai quesiti come quello dell’esempio non è tanto saper fare i calcoli o conoscere specifiche regole matematiche, ma saper utilizzare gli strumenti messi a disposizione dalla literacy matematica per trovare la soluzione utilizzando unità di misura non convenzionali, in questo caso una bottiglia e un bicchiere.
Un altro punto interessante di questo tipo di quesito, che prevede una risposta aperta, è che non si chiede di dare una risposta, ma di dire se si è d’accordo o meno con la risposta di qualcun altro e spiegarne il motivo.
Questo è un aspetto legato al traguardo specifico previsto per quest’ultimo esempio, che richiede di sostenere le proprie idee e confrontarsi con il punto di vista altrui.
Le implicazioni nella formulazione di questo tipo di risposta aperta sono molteplici e sono tutte fortemente legate sia a ciò che prevedono le Indicazioni nazionali e le Linee guida del MIUR sia ad alcune delle skills del 21° secolo su cui si basa la literacy matematica.
Una buona pratica
Come si può intuire da questi esempi, c’è uno studio profondo e una scelta accurata dietro la formulazione di ogni quesito delle Prove INVALSI.
Per questo motivo, il modo migliore per prendere confidenza con i quesiti delle Prove, è affidarsi agli esempi ufficiali messi a disposizione dall’Istituto.
Oltre agli esempi di prove cartacee, sono disponibili online anche degli esempi simulati sulla piattaforma TAO per le classi che svolgono le prove in modalità CBT, ovvero al computer.
Approfondimenti
- Quadro di Riferimento delle Prove INVALSI di Matematica
- Indicazioni nazionali e nuovi scenari del 2017
- PISA for Development Assessment and Analytical Framework
Figure tratte da: Quadro di Riferimento delle Prove INVALSI di matematica


