Che cosa distingue un quesito di una Prova INVALSI da quelli che si trovano sui libri di testo? E che cosa può insegnare la sua complessa preparazione a chi lavora nella scuola?

Preparare un quesito di una Prova INVALSI di Matematica sembra facile.
Non ha l’aria di essere così diverso dagli infiniti esercizi che si trovano sui libri di testo, o che qualsiasi insegnante può aver preparato per i suoi studenti.
In realtà, un quesito INVALSI ha alle spalle una preparazione molto più complessa. Non deve solo misurare una competenza molto precisa, e solo quella. Deve anche essere in grado di evidenziare diversi livelli di quella competenza, dal più basso al più alto. E soprattutto, dobbiamo esserne certi, prima di poterlo inserire in una prova nazionale.
Riuscirci non è affatto banale, al punto che neppure l’esperienza di un bravissimo insegnante può essere sufficiente. Ogni quesito, in fondo, è solo un’ipotesi su che cosa è in grado di fare, e su come ragiona, un gruppo di studenti.
L’esperienza di oltre dieci anni di preparazione delle prove INVALSI ha dimostrato che sbagliare la formulazione di un quesito è facile, e che per questo l’esperienza didattica ha bisogno del riscontro di una o più verifiche sul campo e di una raffinata analisi statistica.
Come nasce un quesito
Il modo migliore per rendersene conto è ripercorrere la storia di un quesito vero. Come se fosse la storia di un esperimento scientifico.
Vi proponiamo l’iter di un quesito presente nella prova di terza secondaria di primo grado, la vecchia terza media, di qualche anno fa. Eccolo nella sua prima formulazione, proposta dal gruppo degli autori di Matematica INVALSI:
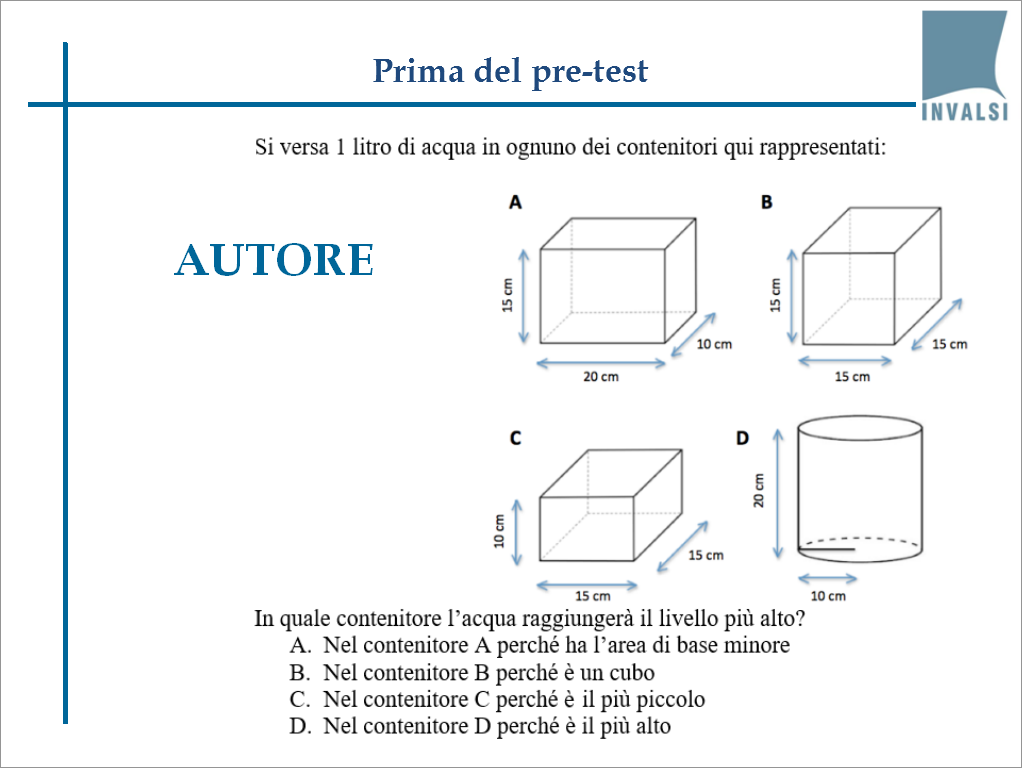
Perché gli autori – un gruppo di insegnanti di grande esperienza – hanno scelto questo problema?
Perché permette di testare una delle competenze previste dal Quadro di Riferimento di Matematica elaborati dall’INVALSI in base alle Indicazioni nazionali: il concetto di volume come prodotto dell’area di base per l’altezza.
Il quesito appartiene all’ambito Spazio e figure, esaminato dal punto di vista della risoluzione di un problema. In particolare, si voleva verificare se i ragazzi avessero chiaro il concetto che, a parità di volume, area di base e altezza sono inversamente proporzionali.
Delle quattro risposte una è corretta, mentre le altre tre – i cosiddetti distrattori in gergo specialistico – devono intercettare errori o fraintendimenti comuni per poter distinguere livelli di abilità diversi. La domanda è molto interessante perché è ricca di elementi matematici e ogni risposta sbagliata appare – per così dire – sbagliata in maniera diversa.
Può funzionare così?
Un gruppo di esperti della disciplina che esamina il quesito decide però per una nuova formulazione, questa:
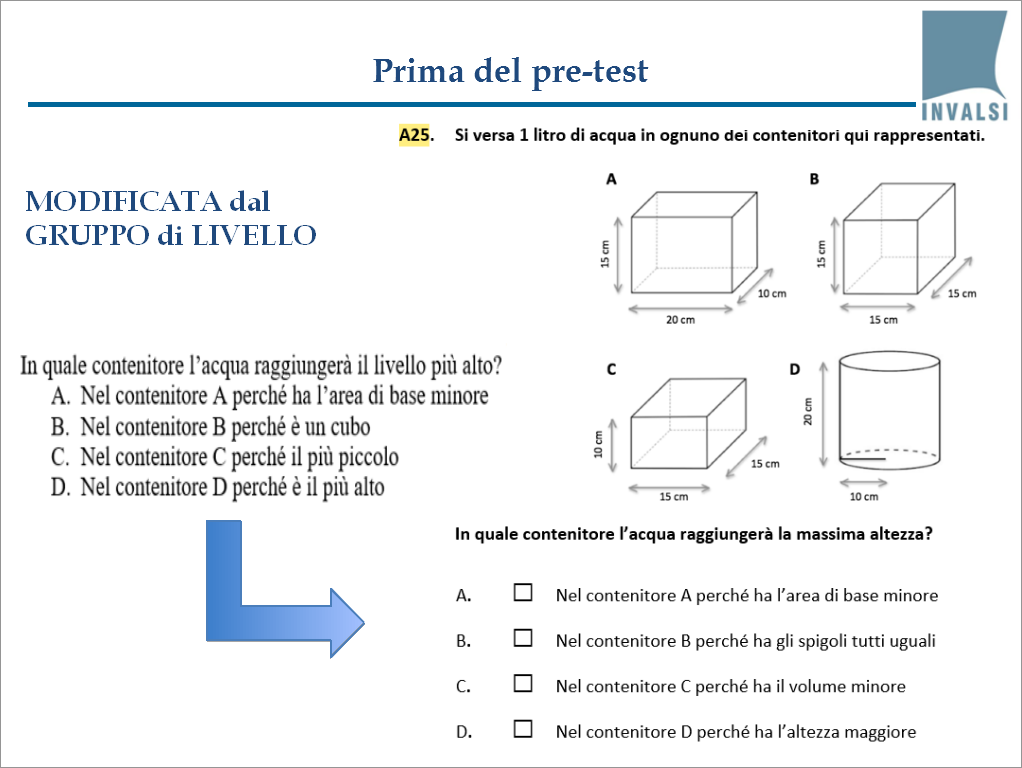
Perché? Il primo motivo è che così il linguaggio è più propriamente matematico, e può evitare che nella misura della competenza geometrica possa interferirne un’altra, che è quella di saper passare da un linguaggio informale e a volte ambiguo a uno formale.
Il secondo motivo è evitare l’ulteriore distrazione costituita da frasi di struttura e lunghezza diverse, che in indagini precedenti è risultata un fattore distraente non trascurabile. Lo scopo – lo ricordiamo – è quello di misurare una competenza precisa, e solo quella. Proprio per questo, ripensandoci, questa seconda formulazione appare senz’altro migliore.
Ma sarà proprio quella giusta?
Facciamo un controllo
Un’analisi didattica può produrre una buona ipotesi, ma come ogni ipotesi deve essere testata nella realtà, prima di poter essere accettata. Il quesito deve essere proposto a un campione rappresentativo di ragazzi, nell’ambito di una prova completa.
E i risultati devono essere analizzati utilizzando gli strumenti della statistica. Insomma, si deve fare uno studio psicometrico. L’INVALSI sottopone infatti a uno o a volte anche due pre-test di questo tipo tutti i quesiti, prima di proporli nelle classi da esaminare.
Nelle analisi psicometriche dell’INVALSI si prendono in considerazione più elementi, di cui esaminiamo qui solo i principali.
Poiché il quesito deve essere in grado di distinguere i diversi livelli di abilità dei ragazzi, ci deve essere una buona correlazione fra la risposta scelta – alla quale, lo ricordiamo, deve corrispondere un certo livello di difficoltà – e il risultato di ogni studente all’intera prova, che ne indica il livello di competenza complessivo.
Gli studenti più bravi dovranno infatti scegliere soprattutto la risposta corretta, e quelli via via meno bravi quelle via via più sbagliate.
Ogni risposta deve poi essere scelta da una certa percentuale di ragazzi. Se la maggior parte risponde correttamente, il quesito è troppo facile.
Se non ci riesce quasi nessuno, o se troppo pochi fra i più bravi rispondono correttamente, vuol dire che è troppo difficile. E così via.
In pratica, si verifica che la distribuzione delle risposte si avvicini a quella ideale di un particolare modello statistico:
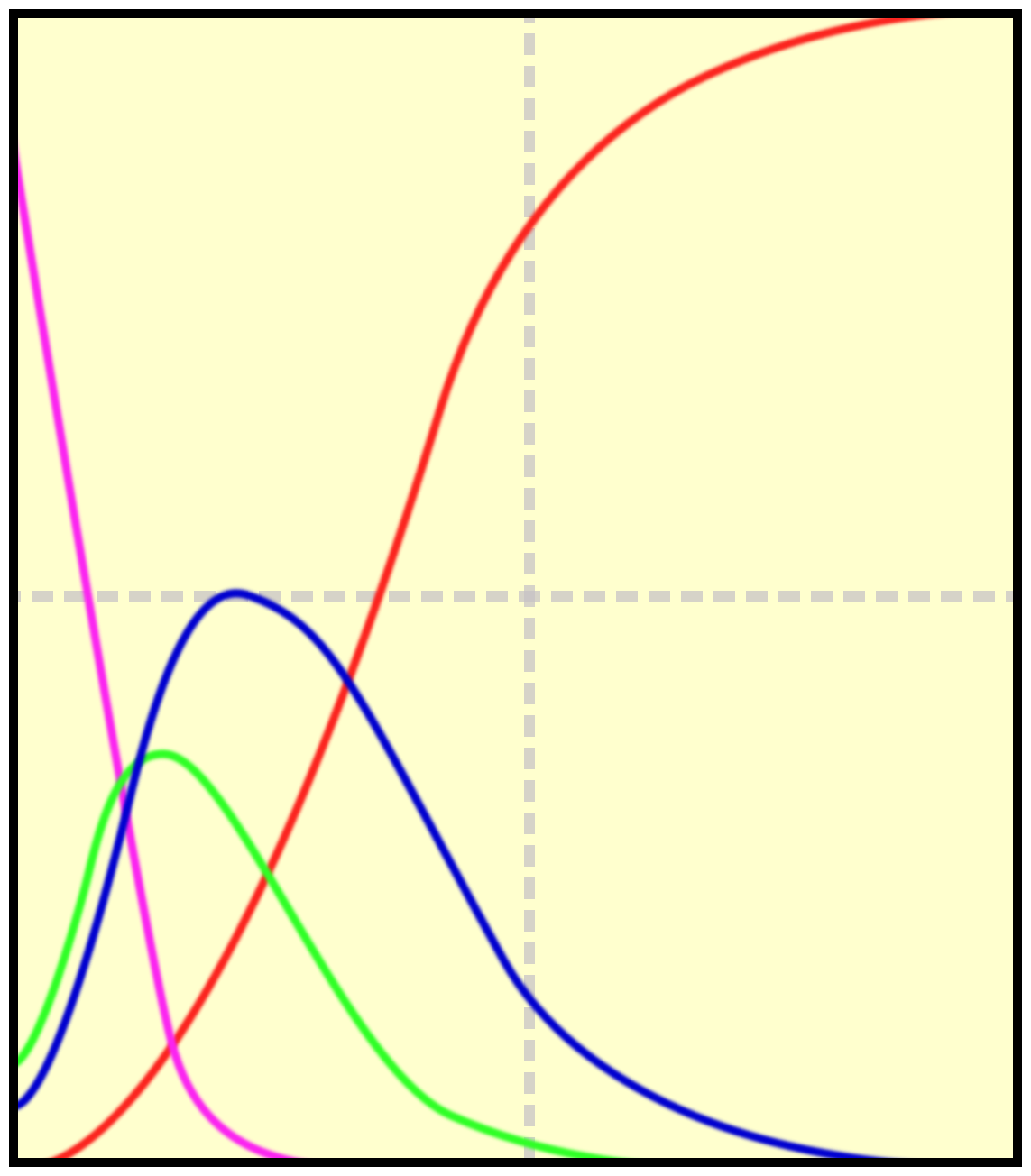
Sull’asse orizzontale c’è la distribuzione dell’abilità degli studenti, ordinati dal meno bravo al più bravo. Su quello verticale c’è la probabilità di scegliere una delle quattro risposte, rappresentate dalle curve colorate.
La curva rossa rappresenta la probabilità di scegliere la risposta corretta in base all’abilità dei ragazzi: come ci si deve aspettare, è bassa fra i meno bravi, e cresce gradualmente fino a raggiungere il massimo fra i più bravi. Da un certo punto in poi ci deve essere solo lei: se un ragazzo è veramente bravo, molto probabilmente sceglierà la risposta corretta.
La curva lilla è quella della risposta più sbagliata: ha la massima probabilità di essere scelta dai meno bravi in assoluto, che diminuisce rapidamente al crescere dell’abilità dei ragazzi. Le altre due curve intercettano livelli di abilità intermedie.
Analizziamo i risultati
Testato su un campione rappresentativo di 389 studenti nell’ambito dei pre-test cui sono sottoposte tutte le Prove INVALSI, il nostro quesito geometrico ha prodotto le seguenti distribuzioni di risposte:
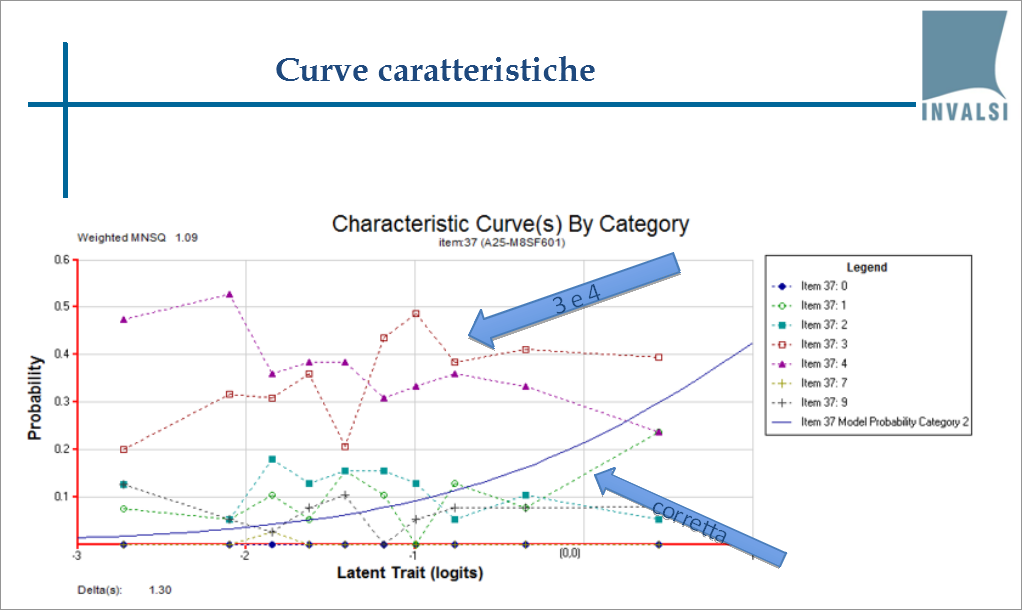
Che cosa ci dicono? Che il quesito non funziona bene.
Innanzitutto è difficile, perché pochi ragazzi scelgono la risposta esatta, rappresentata dalla curva verde. Per di più il loro numero non varia molto passando dai ragazzi risultati complessivamente meno bravi a quelli più bravi.
La distribuzione della risposta 2 è poi troppo simile a quella della risposta 1, quella corretta, quindi non distingue adeguatamente fra chi è più bravo a rispondere e chi è meno bravo.
Infine, troppi ragazzi – e troppi ragazzi bravi – hanno scelto le risposte sbagliate 3 e 4. Insomma, nonostante fosse sembrato molto ben fatto, così com’è il quesito non può entrare a far parte della Prova INVALSI.
Che fare? Buttare via il quesito è un peccato, perché il contenuto matematico – il significato di volume – è molto importante.
Aggiustiamo il tiro
Cosa c’è che non va? Esperti di didattica e psicometristi tornano a sedersi intorno a un tavolo per capirlo, la domanda viene modificata e il risultato è il seguente:

All’apparenza il quesito sembra decisamente impoverito, invece nella nuova versione è stato focalizzato meglio il suo scopo.
In questa formulazione, sono stati cambiati i contenitori in modo tale che abbiano tutti la stessa altezza e quindi questa non induca in confusione, dal momento che l’altezza da considerare è invece quella del liquido – e un ragazzo di terza media forse non lo coglie facilmente.
Così l’attenzione viene indirizzata sull’aspetto veramente importante, cioè sull’area di base. È stato anche modificato il testo della domanda – livello dell’acqua al posto di altezza del contenitore – e sono state tolte le giustificazioni, nell’ipotesi che così i ragazzi si concentreranno sullo specifico contenuto geometrico.
Così formulato, il quesito funzionerà meglio? Per scoprirlo, bisogna sottoporre anche questa ipotesi a un secondo pre-test.
Un altro test
Ecco il risultato: un bel grafico con tutte le curve al loro posto, che mostrano un andamento corretto sia della risposta esatta, sia di quelle errate.
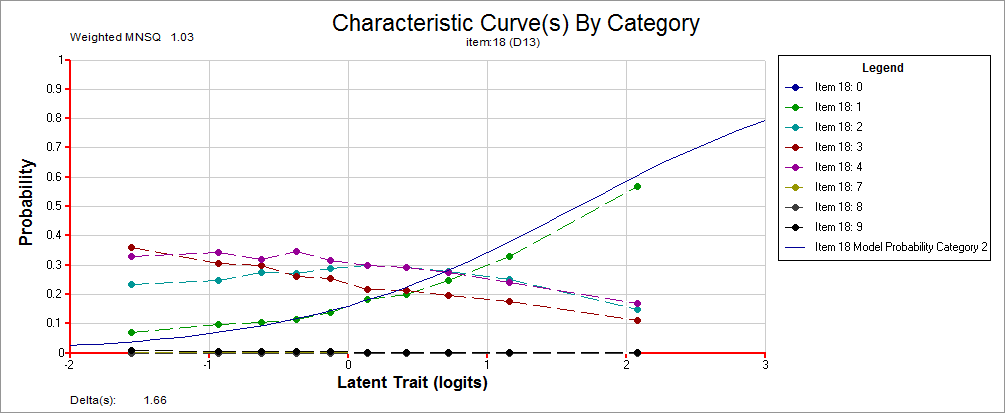
La curva verde, quella della risposta corretta, corre vicinissima a quella azzurra continua, che rappresenta la curva ideale: la probabilità di rispondere correttamente aumenta all’aumentare del livello di abilità dei ragazzi.
Le tre curve delle risposte sbagliate indicano che ciascuna è stata scelta principalmente da studenti di abilità bassa e che all’aumentare dell’abilità, diminuisce la probabilità che lo studente scelga quel tipo di risposta.
Così formulato il quesito è stato inserito nella Prova nazionale.
Cosa ci insegna un quesito
Che cosa ci dice questa breve biografia di un quesito, anche se si tratta solo di un esempio, e anche un po’ semplificato rispetto alla reale complessità di tutti i parametri statistici che sono stati realmente utilizzati?
Ci dice che la valutazione può essere un esercizio molto più difficile di quanto immaginiamo, e costringe soprattutto a pensare molto bene a che cosa esattamente vogliamo valutare.
Ma ci apre anche una piccola finestra sulla complessità del compito svolto dagli insegnanti e dai ricercatori – esperti disciplinari, psicologi, psicometristi, statistici – che lavorano per l’INVALSI.
Compito del quale è facile non rendersi conto se non si conosce il processo di costruzione di una prova stardardizzata.
Approfondimenti
- Cos’è la literacy matematica
- La literacy matematica – Qualche esempio pratico
- La Prova di Italiano della Scuola primaria vista da vicino
Se hai trovato interessante questo contenuto puoi iscriverti alla newsletter mensile di INVALSIopen per ricevere via mail i nostri aggiornamenti.
Voglio ricevere gli aggiornamenti di INVALSIopen


